主成分分析です。
高次元データに対して、ばらつきが大きくなる方向を見極め、次元を落とす方法です。
まずはサンプルデータを作ってプロットしてみます
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
%matplotlib inline # 主成分分析 principal component analysis,PCA import numpy as np import matplotlib.pyplot as plt # サンプルデータの作成 np.random.seed(0) X = np.random.random(size=50) Y = 2 * X + 0.5 * np.random.rand(50) # サンプルデータの可視化 fig, ax = plt.subplots() ax.scatter(X,Y) plt.show() |
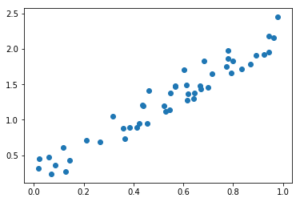
で、これを主成分分析すると
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 主成分分析(PCA)のインスタンスを作成する from sklearn.decomposition import PCA pca = PCA(n_components=2) ''' PCA(copy=True, iterated_power='auto', n_components=2, random_state=None, svd_solver='auto', tol=0.0, whiten=False) ''' # 主成分分析を実行 X_pca = pca.fit_transform(np.hstack((X[:,np.newaxis], Y[:, np.newaxis]))) # 主成分分析結果を可視化する fig, ax =plt.subplots() ax.scatter(X_pca[:, 0], X_pca[:, 1]) ax.set_xlabel('PC1') ax.set_ylabel('PC2') ax.set_xlim(-1.1, 1.1) ax.set_ylim(-1.1, 1.1) plt.show() |

となり、軸PC1方向にデータは散らばっているが軸PC2にはあまり散らばっていないことがわかるわけです。って、可視化すると当たり前ですよね・・・。
いずれ必要になったときに、次元削減関係は深堀りしていきますので、今日はただのメモ書きになりました。