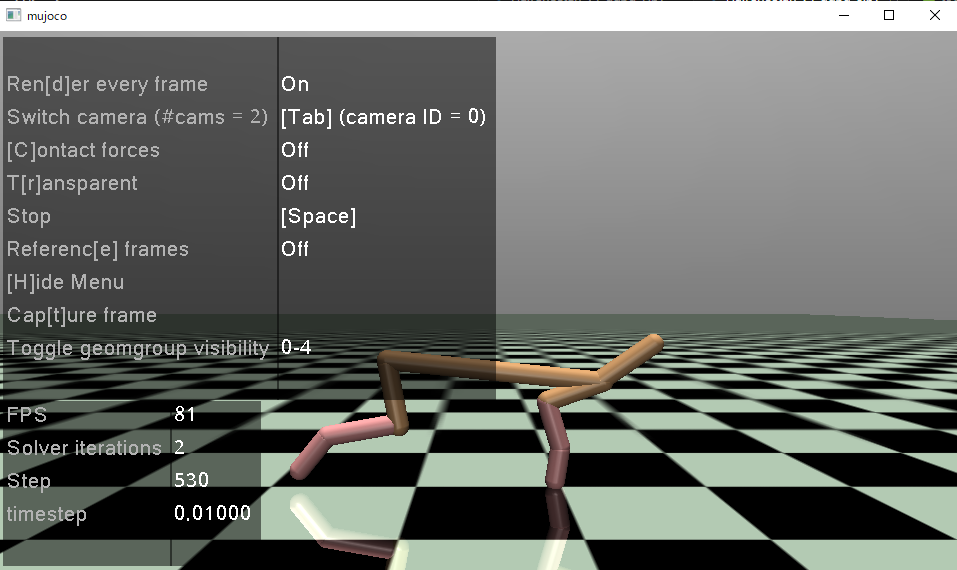
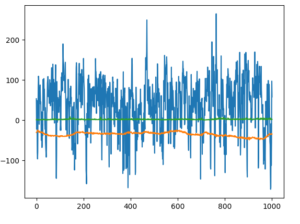
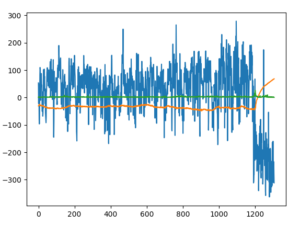
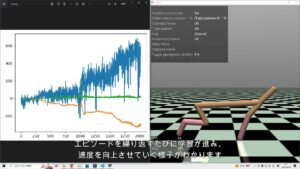
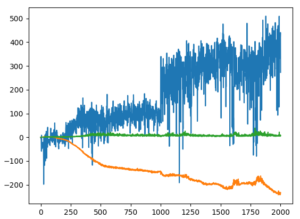
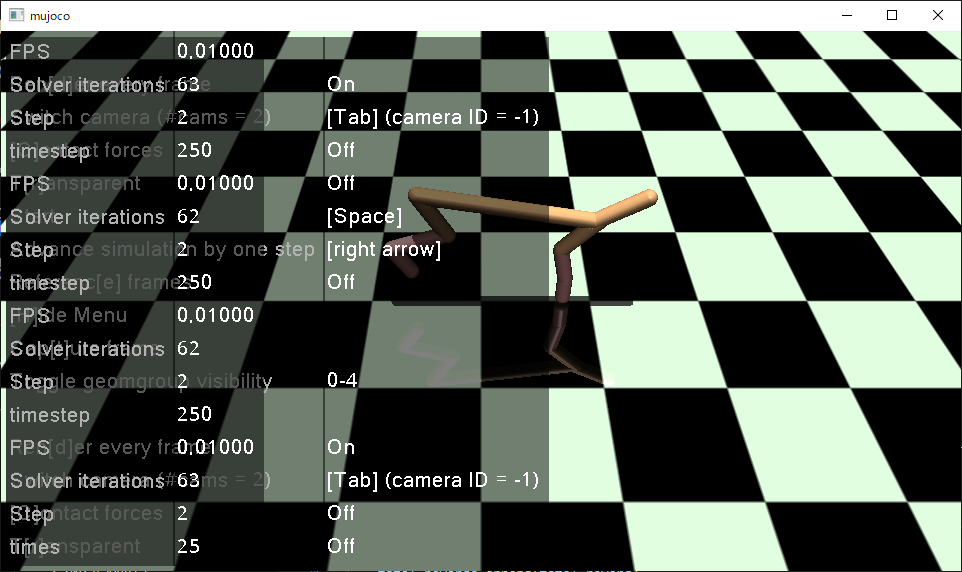
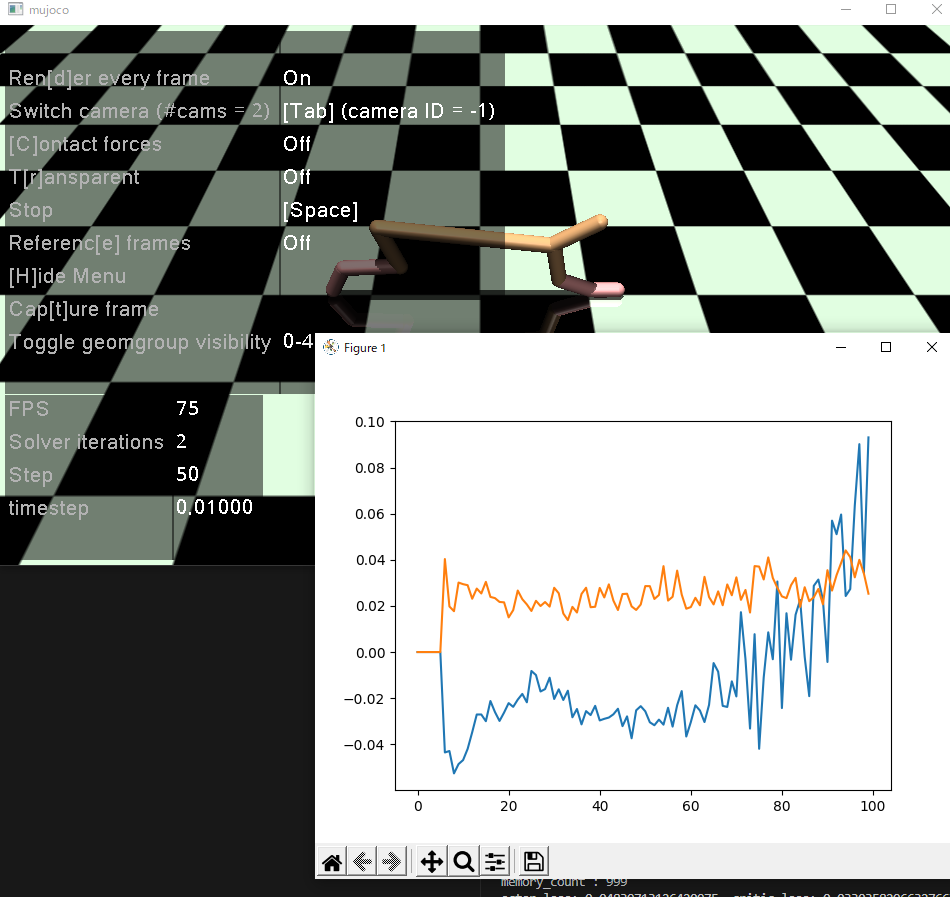
今回は、単純にノードを64から32に落としてみたらどうかと思います。
学習のステップ
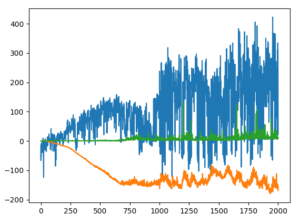
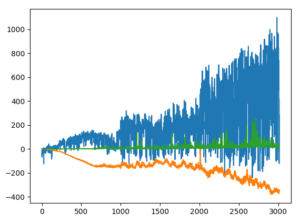
- 100Steps x 1000Epsodes
- 200Steps x 1000Epsodes
- 300Steps x 1000Epsodes
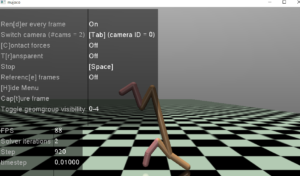
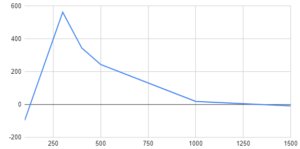
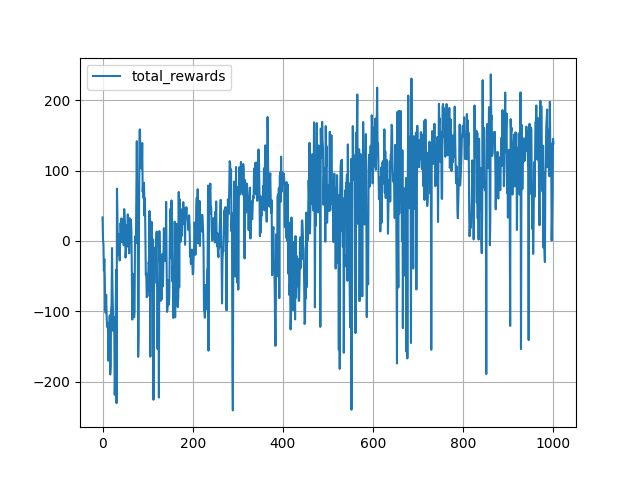
非常にうまくいきました。文句なしです。
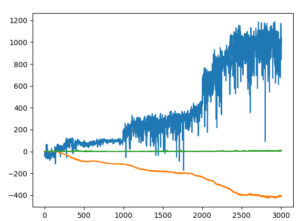
走りも安定しています。
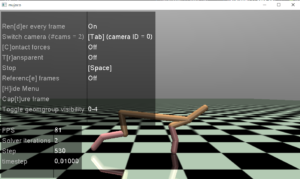
これで、このDDPGシリーズはお終いにいたします。
続編はMalti Agent Deep Detarministic Policy Gradient:MADDPG の予定です。ありがとうございました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 |
import gymnasium as gym import time import torch as T import torch.nn as nn import torch.nn.functional as F import torch.optim as optim import numpy as np import matplotlib.pyplot as plt import os import csv # 44.OUActionNOoiseクラスを作成する class OUActionNoise(object): def __init__(self, mu, sigma=0.15, theta=0.2, dt=1e-2, x0=None): self.mu = mu self.sigma = sigma self.theta = theta self.dt = dt self.x0 = x0 self.reset() def __call__(self): x = self.x_prev + self.theta * (self.mu - self.x_prev) * self.dt + \ self.sigma * np.sqrt(self.dt) * np.random.normal(size=self.mu.shape) self.x_prev = x return x def reset(self): self.x_prev = self.x0 if self.x0 is not None else np.zeros_like(self.mu) # 10. ReplayBufferクラスを新規作成する class ReplayBuffer: def __init__(self, max_memory_size, n_obs_space, n_action_space): self.max_memory_size = max_memory_size self.n_obs_space = n_obs_space self.n_action_space = n_action_space self.memory_count = 0 self.state_memory = np.zeros((self.max_memory_size, self.n_obs_space)) self.action_memory = np.zeros((self.max_memory_size, self.n_action_space)) self.reward_memory = np.zeros(self.max_memory_size) self.next_state_memory = np.zeros((self.max_memory_size, self.n_obs_space)) self.terminal_memory = np.zeros(self.max_memory_size) #self.terminal_memory = np.zeros(self.max_memory_size, dtype=np.bool) # 11.トランジション保存のためstore_transitionメソドを作成する def store_transition(self, obs, action, reward, next_state, done): #print('store_transition is working.') index = self.memory_count % self.max_memory_size # 最大メモリー数に到達したら、古いデータから上書きされていくギミック #print('obs.detach().numpy().flatten():',obs.detach().numpy().flatten()) self.state_memory[index] = obs.detach().numpy().flatten() self.action_memory[index] = action.flatten() self.reward_memory[index] = reward.flatten() self.next_state_memory[index] = next_state.flatten() self.terminal_memory[index] = 1 - int(done) # ゴールならterminal = 0 となるように self.memory_count += 1 #print('memory_count :', agent.memory.memory_count) # 16 バッファメモリーからランダムに抽出する def sample_buffer(self, batch_size): # indexが最大メモリに到達していない場合を想定する。 max_index = min(self.max_memory_size, self.memory_count) choosed_index = np.random.choice(max_index, batch_size) observations = self.state_memory[choosed_index] actions = self.action_memory[choosed_index] rewards = self.reward_memory[choosed_index] next_states = self.next_state_memory[choosed_index] terminals = self.terminal_memory[choosed_index] return observations, actions, rewards, next_states, terminals # 6.ActorNNクラスを新規作成する class ActorNN(nn.Module): def __init__(self, device, alpha=0.001, n_obs_space=17, n_action_space=6, layer1_size=256, layer2_size=256, layer3_size=256, batch_size=64): #print('ActorNN.__init__ is working.') super(ActorNN, self).__init__() self.fc1 = nn.Linear(n_obs_space, layer1_size) f1 = 1 / np.sqrt(self.fc1.weight.data.size()[0]) # Heの初期値 nn.init.uniform_(self.fc1.weight, -f1, +f1) # 重み初期値 -fから+fの範囲で一様分布 nn.init.uniform_(self.fc1.bias, -f1, +f1) # バイアス初期値 -fから+fの範囲で一様分布 self.bn1 = nn.LayerNorm(layer1_size) #レイヤーノーマライゼーション self.fc2 = nn.Linear(layer1_size, layer2_size) f2 = 1 / np.sqrt(self.fc2.weight.data.size()[0]) # Heの初期値 nn.init.uniform_(self.fc2.weight, -f2, +f2) # -fから+fの範囲で一様分布 nn.init.uniform_(self.fc2.bias, -f2, +f2) # -fから+fの範囲で一様分布 self.bn2 = nn.LayerNorm(layer2_size) #レイヤーノーマライゼーション self.fc3 = nn.Linear(layer2_size, n_action_space) # #26.最適化処理としてアダムを設定する self.optimizer = optim.Adam(self.parameters(), lr=alpha) #self.optimizer = optim.SGD(self.parameters(), lr=alpha) def forward(self, obs): #print('AgetDDPG.ActorNN.forward is working') #print('====ここまではOK1====') x = self.fc1(obs) x = self.bn1(x) x = F.relu(x) x = self.fc2(x) x = self.bn2(x) x = F.relu(x) x = self.fc3(x) action = F.tanh(x) return action # 22.CriticNNクラスを新規作成する class CriticNN(nn.Module): def __init__(self, device, beta=0.001, n_obs_space=17, n_action_space=6, layer1_size=256, layer2_size=256, layer3_size=256, batch_size=64): #print('CriticNN.__init__ is working.') super(CriticNN, self).__init__() # クリティックNNは観察空間+行動空間の2つを入力とする構造 input_dim = n_obs_space + n_action_space self.fc1 = nn.Linear(input_dim, layer1_size) f1 = 1 / np.sqrt(self.fc1.weight.data.size()[0]) # Heの初期値 nn.init.uniform_(self.fc1.weight, -f1, +f1) # 重み初期値 -fから+fの範囲で一様分布 nn.init.uniform_(self.fc1.bias, -f1, +f1) # バイアス初期値 -fから+fの範囲で一様分布 self.bn1 = nn.LayerNorm(layer1_size) #レイヤーノーマライゼーション self.fc2 = nn.Linear(layer1_size, layer2_size) f2 = 1 / np.sqrt(self.fc2.weight.data.size()[0]) # Heの初期値 nn.init.uniform_(self.fc2.weight, -f1, +f1) # 重み初期値 -fから+fの範囲で一様分布 nn.init.uniform_(self.fc2.bias, -f1, +f1) # バイアス初期値 -fから+fの範囲で一様分布 self.bn2 = nn.LayerNorm(layer2_size) #レイヤーノーマライゼーション self.fc3 = nn.Linear(layer2_size, 1) # 最後は1個で良い #27.最適化処理としてアダムを設定する self.optimizer = optim.Adam(self.parameters(), lr=beta) #self.optimizer = optim.SGD(self.parameters(), lr=beta) def forward(self, obs, action): input_data = T.cat([obs, action], dim=1) x = self.fc1(input_data) x = self.bn1(x) x = F.relu(x) x = self.fc2(x) x = self.bn2(x) x = F.relu(x) x = self.fc3(x) return x #一つの状態価値を出力する。 # 3.エージェントクラスを定義する class AgentDDPG: def __init__(self, device, alpha=0.000025, beta=0.00025, gamma=0.99, tau=0.001, n_obs_space=17 , n_action_space=6, n_state_action_value=1, layer1_size=64, layer2_size=64, layer3_size=64, batch_size=64, mode='train_mode'): #print('AgentDDPG.__init__ is working.') # 5.ActorNNクラスのインスタンスを生成する self.device = device self.alpha = alpha self.beta = beta self.gamma = gamma self.tau = tau self.n_obs_space = n_obs_space self.n_action_space = n_action_space self.n_state_action_value = n_state_action_value self.layer1_size = layer1_size self.layer2_size = layer2_size self.layer3_size = layer3_size # 13.バッチサイズを決めておく self.batch_size = batch_size self.actor = ActorNN(device=self.device, alpha=self.alpha, n_obs_space=self.n_obs_space, n_action_space=self.n_action_space, layer1_size=self.layer1_size, layer2_size=self.layer2_size, layer3_size=self.layer3_size, batch_size=self.batch_size) if os.path.isfile('actor_params.pt'): # パラメータファイルが存在する場合はロード self.actor.load_state_dict(T.load('actor_params.pt', map_location=device)) print("パラメータファイルをロードしました:", 'actor_params.pt') else: print("パラメータファイルが見つかりません:", 'actor_params.pt') # actorネットワークをGPUへ転送 self.actor.to(device) # 9.memoryインスタンスを追加 self.MAX_MEMORY_SIZE = 10000 self.memory = ReplayBuffer(max_memory_size=self.MAX_MEMORY_SIZE, n_obs_space=self.n_obs_space, n_action_space=self.n_action_space) # 19.ターゲットアクターネットワークインスタンスtarget_actorを作成する # actorとtarget_actorのネットワークは同じActorNNで良い self.target_actor = ActorNN(device=self.device, alpha=self.alpha, n_obs_space=self.n_obs_space, n_action_space=self.n_action_space, layer1_size=self.layer1_size, layer2_size=self.layer2_size, layer3_size=self.layer3_size, batch_size=self.batch_size) if os.path.isfile('target_actor_params.pt'): # パラメータファイルが存在する場合はロード self.target_actor.load_state_dict(T.load('target_actor_params.pt', map_location=device)) print("パラメータファイルをロードしました:", 'target_actor_params.pt') else: print("パラメータファイルが見つかりません:", 'target_actor_params.pt') # target_actorネットワークをGPUへ転送 self.target_actor.to(device) # 21.ターゲットクリティックネットワークインスタンスtareget_criticを作成する self.target_critic = CriticNN(device=self.device, beta=self.beta, n_obs_space=self.n_obs_space, n_action_space=self.n_action_space, layer1_size=self.layer1_size, layer2_size=self.layer2_size, layer3_size=self.layer3_size, batch_size=self.batch_size) if os.path.isfile('target_critic_params.pt'): # パラメータファイルが存在する場合はロード self.target_critic.load_state_dict(T.load('target_critic_params.pt', map_location=device)) print("パラメータファイルをロードしました:", 'target_critic_params.pt') else: print("パラメータファイルが見つかりません:", 'target_critic_params.pt') # target_criticネットワークをGPUへ転送 self.target_critic.to(device) # 24.クリティックネットワークインスタンスcriticを作成する。 self.critic = CriticNN(device=self.device, beta=self.beta, n_obs_space=self.n_obs_space, n_action_space=self.n_action_space, layer1_size=self.layer1_size, layer2_size=self.layer2_size, layer3_size=self.layer3_size, batch_size=self.batch_size) if os.path.isfile('critic_params.pt'): # パラメータファイルが存在する場合はロード self.critic.load_state_dict(T.load('critic_params.pt', map_location=device)) print("パラメータファイルをロードしました:", 'critic_params.pt') else: print("パラメータファイルが見つかりません:", 'critic_params.pt') # criticネットワークをGPUへ転送 self.critic.to(device) # アクターロスとクリティックロス self.actor_loss = 0 self.critic_loss = 0 # 45.行動ノイズのインスタンス化 self.mode = mode if self.mode == 'train_mode': self.noise = OUActionNoise(mu=np.zeros(n_action_space)) elif self.mode == 'eval_mode': self.noise = OUActionNoise(mu=np.zeros(n_action_space), sigma=0) else: print('mode error') def choose_action(self, obs): # GPU対応済み #print('AgentDDPG.choose_action is working.') # 4.方策(アクター)はニューラルネットワークで表現する。 # ActorNNクラスを新規作成し、インスタンスactorとして使用する。 obs = obs.to(device) action = self.actor.forward(obs) action = action.cpu() # 46.行動ノイズを入れて探索性を向上させる。 action += T.tensor(self.noise(), dtype=T.float32) action = action.detach().numpy() return action # 8.remenberメソドを追加 def remember(self, obs, action, reward, next_state, done): self.memory.store_transition(obs, action, reward, next_state, done) # 13.learnメソドを追加 def learn(self): # 14.バッチサイズ分のトランジションが集まるまでは何も実行しない。 if self.memory.memory_count < self.batch_size: return # 15.メモリバッファからデータを抜き出す sample_buffer() # バッチ化されているので変数名を複数形にする observations, actions, rewards, next_states, terminals = self.memory.sample_buffer(self.batch_size) # 17.抜き出したデータをpytorchで微分可能なようにtorch.tensor化する observations = T.tensor(observations, dtype=T.float32).to(device) actions = T.tensor(actions, dtype=T.float32).to(device) rewards = T.tensor(rewards, dtype=T.float32).to(device) next_states = T.tensor(next_states, dtype=T.float32).to(device) terminals = T.tensor(terminals, dtype=T.float32).to(device) # 18.ターゲットアクターネットワークインスタンスtarget_actorに # 次の状態next_satesを入れて、ターゲットアクションtarget_actionsとして取り出す。 # このターゲットネットワークはターゲットでないネットワークとNNパラメータを共有させる。 #print('next_states :', next_states) target_actions = self.target_actor.forward(next_states) # 20.ターゲットクリティックネットワークインスタンスtarget_criticに # 次の状態next_statesと上記より算出したターゲットアクションの2つを入力して # 価値関数の推定値ターゲットバリューを出力する。 # TDターゲット:r + γ*V(w)[s_t+1] の部分のこと。 # ターゲットクリティックバリューはターゲットアクターネットワークを使う target_critic_values = self.target_critic.forward(next_states, target_actions) # 23.ベースラインとして機能するクリティックネットワーク(価値関数V(w)[s_t]ネットワーク)に # 現在の状態observationsと行動actionsを入力して # クリティックバリューを算出する critic_values = self.critic.forward(observations, actions) # 25.TDターゲットを算出する:r + γ*V(w)[s_t+1] td_targets = [] for i in range(self.batch_size): td_target = rewards[i] + self.gamma * target_critic_values[i] * terminals[i] td_targets.append(td_target) # TDターゲットの形をバッチに整える td_targets = T.tensor(td_targets, dtype=T.float32).to(device) td_targets = td_targets.view(self.batch_size, 1) #viewはreshapeと同じ。64x1に見え方を変更した、という意味 #print('td_targets :', td_targets) # ==== (1)クリティックの学習 ==== # 28.クリティックの勾配をゼロに初期化する self.critic.optimizer.zero_grad() # 29. TDターゲットと状態価値の二乗誤差を算出して、クリティックの損失関数とする。バッチサイズは64個 critic_loss = F.mse_loss(td_targets, critic_values) self.critic_loss = critic_loss #print('critic_loss : ', critic_loss) # tensor(0.0485, grad_fn=<MseLossBackward0>) # 30. クリティックの損失関数を微分して、勾配を算出する self.critic_loss.backward() # 31. 勾配からオプティマイザーによってクリティックのパラメータ(重みとバイアス)を更新する self.critic.optimizer.step() # ==== (2)アクターの学習 ==== # 32. アクターの勾配をゼロに初期化する self.actor.optimizer.zero_grad() # 33. アクターに観測情報を入力して行動を算出する。バッチサイズは64個 predicted_actions = self.actor.forward(observations) # 34.アクターの損失関数を算出する # Actorの目的は、Criticネットワークの出力(行動価値)を最大化するような行動を選択すること。 # なので、actorNN→criticNNのDDPG構造全体の出力結果をactor_lossとして、actorNNとcriticNNの両方をbackwardし、 # actorだけをパラメータ更新することによりactorの学習をすることができる。 actor_loss = -self.critic.forward(observations, predicted_actions) actor_loss = T.mean(actor_loss) self.actor_loss = actor_loss #print(f'actor_loss: {actor_loss}, critic_loss: {critic_loss}') # 35. DDPG構造全体の損失関数actor_lossを微分し、勾配を算出する self.actor_loss.backward() # 36. 勾配からオプティマイザーによってアクターのパラメータだけを(重みとバイアス)を更新する self.actor.optimizer.step() # 37. 全ニューラルネットワークのパラメータを更新する。 self.update_network_parameters() # 37. パラメータ更新メソド。 def update_network_parameters(self, tau=None): if tau is None: tau = self.tau # 38. actor, critic, target_actor, target_criticのネットワーク内の全てのパラメータ(重みとバイアス)とその名前を取得する # actorとcriticは先ほど更新されたばかりのパラメーター actor_params = self.actor.named_parameters() critic_params = self.critic.named_parameters() target_actor_params = self.target_actor.named_parameters() target_critic_params = self.target_critic.named_parameters() #print('actor_params : ', actor_params) # actor_params : <generator object Module.named_parameters at 0x000001661B2D9D48> # 39. パラメータをディクショナリとして取り出す。 actor_params_dict = dict(actor_params) critic_params_dict = dict(critic_params) target_actor_params_dict = dict(target_actor_params) target_critic_params_dict = dict(target_critic_params) #print('actor_params_dict : ', actor_params_dict) #print(actor_params_dict.keys()) # 40. クリティックの各パラメーター毎に 更新重みtau=0.0001の分だけほんの少しcriticパラメータをtarget_criticパラメータに近づける。 for name in critic_params_dict: critic_params_dict[name] = tau * critic_params_dict[name].clone() + \ (1-tau) * target_critic_params_dict[name].clone() # 41. 更新したcriticパラメータをtarget_criticのパラメータとしてロードする。 self.target_critic.load_state_dict(critic_params_dict) # 42.アクターの各パラメーター毎に 更新重みtau=0.0001の分だけほんの少しactorパラメータをtarget_actorパラメータに近づける。 for name in actor_params_dict: actor_params_dict[name] = tau * actor_params_dict[name].clone() + \ (1 - tau) * target_actor_params_dict[name].clone() # 43. 更新したactorパラメータをtarget_actorのパラメータとしてロードする。 self.target_actor.load_state_dict(actor_params_dict) # データをCSVファイルに追記保存する関数 def append_data_to_csv(episode, total_reward, actor_loss, critic_loss, file_path): with open(file_path, 'a', newline='') as csvfile: writer = csv.writer(csvfile) writer.writerow([episode, total_reward, actor_loss, critic_loss]) #### =================== メインスクリプト ======================= #### device = T.device('cuda' if T.cuda.is_available() else 'cpu') # cuda追加 device = 'cpu' # 強制的にcpuを使う EVAL_TRAIN_MODE = 'eval_mode' # eval_mode 評価モードか train_mode 訓練モードかを選択 EPISODES = 1001 # episodes STEPS = 300 # steps DELAY_TIME = 0.00 # sec print('Selected Mode : ', EVAL_TRAIN_MODE) # 2.エージェントクラスのインスタンスを生成する agent = AgentDDPG(device=device, alpha=0.0001, beta=0.0001, gamma=0.99, tau=0.01, n_obs_space=17 , n_action_space=6, n_state_action_value=1, layer1_size=32, layer2_size=32, layer3_size=32, batch_size=64, mode=EVAL_TRAIN_MODE) # cuda追加 if EVAL_TRAIN_MODE == 'train_mode': env = gym.make("HalfCheetah-v4", render_mode='depth_array') elif EVAL_TRAIN_MODE == 'eval_mode': env = gym.make("HalfCheetah-v4", render_mode= 'human') total_rewards = [] actor_losses = [] critic_losses = [] for episode in range(EPISODES): obs = env.reset() obs = T.tensor(obs[0], dtype=T.float) reward: float = 0 total_reward: float = 0 done: bool = False for j in range(STEPS): env.render() # ここをDDPGに置き換えていく action = agent.choose_action(obs) # 1.Agentクラスを定義していく # GPU対応済み next_state, reward, done, _, info = env.step(action) #print('next_state, reward, done, _, info :', next_state, reward, done, _, info) #7. トラジェクトを保存する。経験再生(ReplayBuffer) agent.remember(obs, action, reward, next_state, int(done)) #12. ニューラルネットワークを学習する agent.learn() # 26.エピソード内での報酬を累積していく total_reward += reward # 27. next_stateをobsとして再出発する #print('next_state:', next_state) obs = next_state obs = T.tensor(obs, dtype=T.float) # 28. チーターの動きを見たいのでスリープを入れる time.sleep(DELAY_TIME) #print('total_reward : ', total_reward) total_rewards.append(total_reward) actor_losses.append(agent.actor_loss) critic_losses.append(agent.critic_loss) # print('epsisode', i, 'score %.2f' % score, '100 game sverage %.2f' % np.mean(score_history[-100:])) # 47. 各ニューラルネットワークのパラメータを10エピソード毎に保存する print('episode, total_reward : ', episode , total_reward, float(agent.actor_loss), float(agent.critic_loss)) if episode % 10 == 0: T.save(agent.actor.state_dict(), 'actor_params.pt') T.save(agent.critic.state_dict(), 'critic_params.pt') T.save(agent.target_actor.state_dict(), 'target_actor_params.pt') T.save(agent.target_critic.state_dict(), 'target_critic_params.pt') print('==== params were saved. ====') append_data_to_csv(episode, total_reward, float(agent.actor_loss), float(agent.critic_loss), 'total_reward.csv') #print('total_rewards : ', total_rewards) #plt.plot(total_rewards) #plt.plot(actor_losses, label='actor_losses') #plt.plot(critic_losses, label='critic_losses') plt.plot(total_rewards, label='total_rewards') plt.legend() plt.grid(True) plt.ioff() plt.show() env.close() # 空なんですけど・・・ print('script is done.') |