やってみよう。
まずは線形回帰
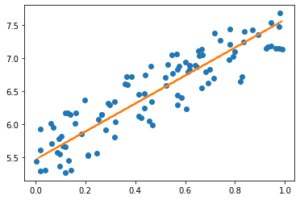
グラフはこんな感じで線形近似できている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
# 線形回帰 %matplotlib inline import numpy as np import matplotlib.pylab as plt import dezero.functions as F from dezero import Variable np.random.seed(0) x = np.random.rand(100,1) y = 5 + 2 *x +np.random.rand(100,1) plt.plot(x,y,'o') x, y = Variable(x), Variable(y) # パラメータはW一つ b一つあればいい W = Variable(np.zeros((1,1))) b = Variable(np.zeros((1))) def predict(x): y = F.matmul(x, W) + b return y def mean_squared_error(x0, x1): diff = x0 - x1 return F.sum(diff ** 2) / len(diff) lr = 0.1 iters = 100 for i in range(iters): # 予測 y_pred = predict(x) # 損失 loss = mean_squared_error(y, y_pred) # 勾配初期化 W.cleargrad() b.cleargrad() # 損失勾配 loss.backward() # 勾配降下法によるパラメータ更新 W.data -= lr * W.grad.data b.data -= lr * b.grad.data if (i % 10) == 0: # 10計算毎に出力をする print(i, loss.data) # 結果表示 print(W.data, b.data) plt.plot(x.data, W.data * x.data + b.data) |
損失が徐々に減っていく。いい感じだ。
|
1 2 3 4 5 6 7 8 9 10 11 |
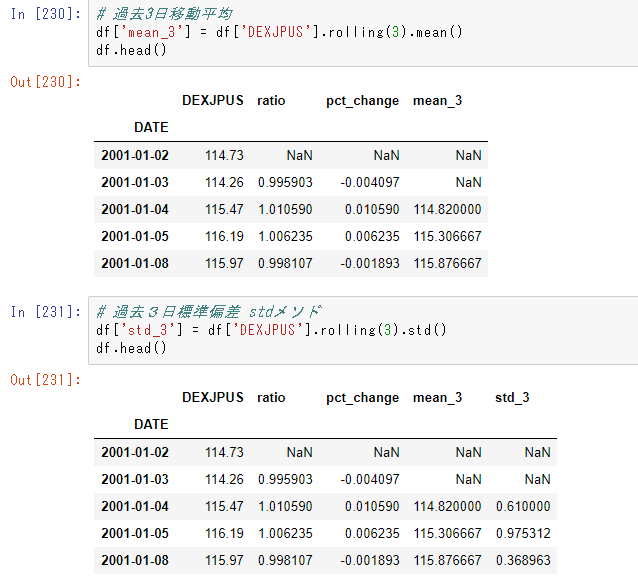
0 42.296340129442335 10 0.24915731977561134 20 0.10078974954301652 30 0.09461859803040694 40 0.0902667138137311 50 0.08694585483964615 60 0.08441084206493275 70 0.08247571022229121 80 0.08099850454041051 90 0.07987086218625004 [[2.11807369]] [5.46608905] |
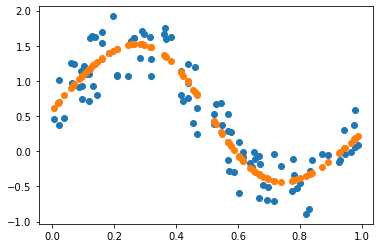
これをsinカーブでやってみると、直線しか表現できないのでぜんぜんだめ
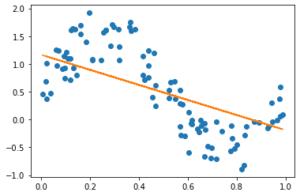
そこでニューラルネットワークの出番。
活性化関数のお陰で表現が増える
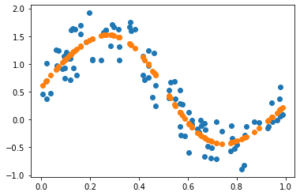
sinカーブにノイズをのせたサンプルデータを作ってニューラルネットワークでやってみよう
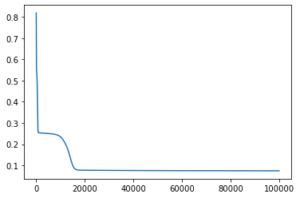
損失の減り方をみると開始直後に急激に減って、なんと1万回くらいのところで再度損失が急激に減少した。理由は分からないが なんかすごい。
ではコードはこちら
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
# ニューラルネットワークで回帰(成功例) import numpy as np import dezero.layers as L # データサンプルを生成 np.random.seed(0) x = np.random.rand(100, 1) # 行x列 y = np.sin(2*np.pi*x)+np.random.rand(100,1) plt.plot(x,y,'o') # dezero変数へ変換 x, y = Variable(x), Variable(y) # NNのパラメータの初期化 I, H, O = 1, 10, 1 W1 = Variable(0.01 * np.random.randn(I, H)) b1 = Variable(np.zeros(H)) W2 = Variable(0.01 * np.random.rand(H, O)) b2 = Variable(np.zeros(O)) # 推論:ニューラルネットワーク def predict(x): y = F.linear(x, W1, b1) y = F.sigmoid(y) y = F.linear(y, W2, b2) return y # 損失関数 def mean_squared_error(x0, x1): diff = x0 - x1 return F.sum(diff ** 2) / len(diff) # 学習 lr = 0.1 iters = 100000 loss_list = [] iters_list = [] for i in range(iters): # 予測 y_pred = predict(x) # 損失 loss = mean_squared_error(y, y_pred) # 勾配初期化 W1.cleargrad() b1.cleargrad() W2.cleargrad() b2.cleargrad() # 損失勾配 loss.backward() # 勾配降下法によるパラメータ更新 W1.data -= lr * W1.grad.data b1.data -= lr * b1.grad.data W2.data -= lr * W2.grad.data b2.data -= lr * b2.grad.data if (i % 1000) == 0: # 10計算毎に出力をする loss_list.append(loss.data) iters_list.append(i) print(i, loss.data) # 結果表示 plt.plot(x.data, predict(x).data, 'o') plt.show() plt.plot(iters_list, loss_list) |
次回予告
次はdezeroをフル活用でやってみよう
オプティマイザとかも予め用意されているらしい。