今日は機械学習モデルの評価について考えてみます。
Contents
機械学習モデルの評価
訓練したモデルに対して、新しいデータが入ってきたときに、データのカテゴリをどれだけ正確に当てられたかが、その訓練済みモデルの性能になりますよね。
カテゴリの分類精として、下記4つの確率的な指標があります。
- 度適合率 Precision = tp / (tp + fp) :予測するクラスをなるべく間違えないようにする指標
- 再現率 Recall = tp / (tp +fn )
- F値 F-Value = 2/((1/適合率)+(1/再現率)) :適合率と再現率の調和平均
- 正解率 (tp+tn)/(tp+fp+fn+tn) :予測と実績が一致したデータの割合
で、これを一つの行列にまとめたのが、
混同行列 Confusion matrix
というものです。
各変数になっていのは
- tp : True-Positive 正例Positiveと予測して、正解Trueだった
- fp : False-Positive 正例Positiveと予測して、不正解Falseだった
- fn : True-Negative 負例Negativeと予測して、正解Trueだった
- tn : False-Negative 負例Negativeと予測して、不正解Falseだった
という結果の数が入ります。
統計用語が入っていますが、
- 正例:興味のある事柄のクラスに属するデータ
- 負例:興味のない事柄のクラスに属するデータ
ということです。
アイリスデータをSVMで分類する
混同行列を見ていきたいので、まずはサンプルデータとしてアイリスデータをSVM分類し、予測結果まで実行してみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
# Irisデータの class0 と class1だけを使って SVMし、混同行列を作ってみる from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.svm import SVC iris = load_iris() iris.keys() # dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename']) # 100データを使用する X, y = iris.data[:100, :], iris.target[:100] # 訓練用データと検証用データに分割する X_train, X_test, y_train, y_test = train_test_split(X, y) # 機械学習モデル(SVC)のインスタンスを作成する svc = SVC() ''' SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, decision_function_shape='ovr', degree=3, gamma='auto_deprecated', kernel='rbf', max_iter=-1, probability=False, random_state=None, shrinking=True, tol=0.001, verbose=False) ''' # 訓練する svc.fit(X_train, y_train) # 予測する y_predicted = svc.predict(X_test) y_predicted y_true = y_test == y_predicted score = sum(y_true) / len(y_true) print('score : ', score) |
混同行列を算出する
基本的には適合率が高いものが優秀と考えています。
再現率も考慮して 適合率と再現率の間を取るのがF1という値です。
|
1 2 3 4 5 |
# 混同行列の算出 (分類レポート) from sklearn.metrics import classification_report # 適合率precision 再現率recall F値f1-score print(classification_report(y_test, y_predicted)) |
|
1 2 3 4 5 6 7 8 |
precision recall f1-score support 0 1.00 1.00 1.00 9 1 1.00 1.00 1.00 16 micro avg 1.00 1.00 1.00 25 macro avg 1.00 1.00 1.00 25 weighted avg 1.00 1.00 1.00 25 |
こんな形のマトリクスで出力されます。
層化k分割交差検証
もともとのデータをk個の塊に等分して、訓練用データと検証用データの組み合わせをkパターン用意して、kパターンすべてについて一気に交差検証をする方法です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 交差検証 Cross Validation # 層化k分割交差検証 Stratified k-fold Cross Validation from sklearn.svm import SVC from sklearn.model_selection import cross_val_score # 機械学習モデル(SVC)のインスタンスを作成する svc = SVC()なので10個 # 層化10分割交差検証を実施する cvs = cross_val_score(svc, X, y, cv=10, scoring='precision') # 適合率(Precision)の結果 10パターンの交差検証なので10個ある print(cvs) # [1. 1. 1. 1. 1. 1. 1. 1. 1. 1.] |
ROCとAUC
予測確率の正確さを見ていく方法です。
- ROC曲線:Receiver Operating Characteristic
- AUC : Area Under the Curve
確率の高い順にデータを並べる
確率以上のデータはすべて正例と予測する
実際に正例だったデータの割合(真陽性率)
実際は負例にも関わらず正例と予測されたデータの割合(偽陽性率)
正例と予測する確率のしきい値を変えていったときに真陽性率を横軸、
偽陽性率を縦軸にとったものがROC曲線
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# ROC曲線 import numpy as np import matplotlib.pyplot as plt #偽陽性率fpr と 真陽性率tpr を計算する fpr = np.array([0,0,0,1,1,2,3,3,3,4,5,5,6,7,8,8,8,9,10,10,11,12,12,13,14])/14 tpr = np.array([1,2,2,3,3,3,4,5,6,6,6,7,7,7,7,8,9,9,9,10,10,10,11,11,11])/11 # ROC曲線を可視化する fig, ax = plt.subplots() ax.step(fpr, tpr) ax.set_xlabel('False Positive rate') ax.set_ylabel('True Positive rate') plt.show() |
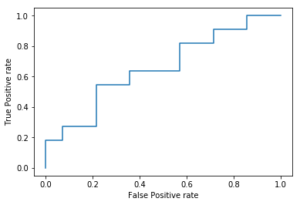
次に AUC曲線 Area Under the Curveですが、要するにROC曲線の面積のことです。1に近いほど正例、0.5に近づくほど正例と負例が混在していて分類できなくなるという意味があります。
ROC曲線と AUCを素早く求めて見ましょう
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
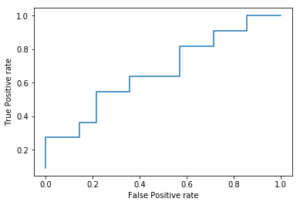
# ROC曲線と AUC曲線を素早く求める from sklearn.metrics import roc_curve # ROC曲線を求めるモジュール # ラベル:各ユーザーが退会したら1 していなかったら0 labels = np.array([1,1,0,1,0,0,1,1,1,0,0,1,0,0,0,1,1,0,0,1,0,0,1,0,0]) # 各ユーザーの予測退会率 probablies = np.array([0.98, 0.95, 0.90, 0.87, 0.85, 0.80, 0.75, 0.71, 0.63, 0.55, 0.51, 0.47, 0.43, 0.38, 0.35, 0.31, 0.28, 0.24, 0.22, 0.19, 0.15, 0.12, 0.08, 0.04, 0.01]) # 偽陽性率fpr 真陽性率tpr しきい値thresholdを算出する fpr, tpr, threshold = roc_curve(labels, probablies) print('fpr : ', fpr) print('tpr : ', tpr) # ROC曲線を可視化する fig, ax = plt.subplots() ax.step(fpr, tpr) ax.set_xlabel('False Positive rate') ax.set_ylabel('True Positive rate') plt.show() # AUCを算出する from sklearn.metrics import roc_auc_score roc_auc_score(labels, probablies) # 0.6558441558441558 |
参考
The following two tabs change content below.


Keita N
最新記事 by Keita N (全て見る)
- 2024/1/13 ビットコインETFの取引開始:新たな時代の幕開け - 2024年1月13日
- 2024/1/5 日本ビジネスにおける変革の必要性とその方向性 - 2024年1月6日
- 2024/1/3 アメリカ債権ETFの見通しと最新動向 - 2024年1月3日